The source files for all examples can be found in /examples.
Example 8: Improving moment estimation
This example will show how to improve the estimation of both low and higher order moments using denoising and sparsification techniques.
using PortfolioOptimisers, PrettyTables
# Format for pretty tables.
tsfmt = (v, i, j) -> begin
if j == 1
return Date(v)
else
return v
end
end;
resfmt = (v, i, j) -> begin
if j == 1
return v
else
return isa(v, Number) ? "$(round(v*100, digits=3)) %" : v
end
end;
mmtfmt = (v, i, j) -> begin
if i == j == 1
return v
else
return isa(v, Number) ? "$(round(v*100, digits=3)) %" : v
end
end;
hmmtfmt = (v, i, j) -> begin
if i == j == 1
return v
else
return isa(v, Number) ? "$(round(v*100*1e4, digits=2))e-4 %" : v
end
end;1. ReturnsResult data
We will use the same data as the previous example.
using CSV, TimeSeries, DataFrames
X = TimeArray(CSV.File(joinpath(@__DIR__, "SP500.csv.gz")); timestamp = :Date)[(end - 252):end]
pretty_table(X[(end - 5):end]; formatters = [tsfmt])
# Compute the returns
rd = prices_to_returns(X)ReturnsResult
nx ┼ 20-element Vector{String}
X ┼ 252×20 Matrix{Float64}
nf ┼ nothing
F ┼ nothing
ts ┼ 252-element Vector{Dates.Date}
iv ┼ nothing
ivpa ┴ nothing2. Prior statistics
Here we will only use empirical priors but with denoising and sparsification techniques applied.
For denoising we will use Denoise, and all its associated algorithms ShrunkDenoise, FixedDenoise, and SpectralDenoise, though the last one may not always produce a matrix with a lower condition number.
For sparsification we will use the relationship structure to sparsify the inverse of the matrix using LoGo with two different distance matrix similarity measures, MaximumDistanceSimilarity and ExponentialSimilarity.
We will also improve the estimation of the mean return by using a shrunk expected returns estimator ShrunkExpectedReturns using BayesStein and BodnarOkhrinParolya algorithms with all three available expected returns shrinkage targets GrandMean, VolatilityWeighted, and MeanSquaredError.
pes = [EmpiricalPrior(;),#
EmpiricalPrior(;
me = ShrunkExpectedReturns(;
alg = BayesStein(;
tgt = VolatilityWeighted())),#
ce = PortfolioOptimisersCovariance(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(;
alg = FixedDenoise())))),#
EmpiricalPrior(;
me = ShrunkExpectedReturns(;
alg = BayesStein(;
tgt = MeanSquaredError())),#
ce = PortfolioOptimisersCovariance(;
mp = DenoiseDetoneAlgMatrixProcessing(;
alg = LoGo()))),
HighOrderPriorEstimator(;
pe = EmpiricalPrior(;
ce = PortfolioOptimisersCovariance(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(;
alg = ShrunkDenoise(;
alpha = 0.5)))),
me = ShrunkExpectedReturns(;
alg = BodnarOkhrinParolya()))),
HighOrderPriorEstimator(;
pe = EmpiricalPrior(;
me = ShrunkExpectedReturns(;
alg = BodnarOkhrinParolya(;
tgt = VolatilityWeighted())),
ce = PortfolioOptimisersCovariance(;
mp = DenoiseDetoneAlgMatrixProcessing(;
alg = LoGo(),
dn = Denoise(;
alg = FixedDenoise())))),
ske = Coskewness(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(;
alg = FixedDenoise()))),
kte = Cokurtosis(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(;
alg = FixedDenoise())))),
HighOrderPriorEstimator(;
pe = EmpiricalPrior(;
me = ShrunkExpectedReturns(;
alg = BodnarOkhrinParolya(;
tgt = MeanSquaredError())),
ce = PortfolioOptimisersCovariance(;
mp = DenoiseDetoneAlgMatrixProcessing(;
alg = LoGo(;
sim = ExponentialSimilarity())))),
ske = Coskewness(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(),
alg = LoGo())),
kte = Cokurtosis(;
mp = DenoiseDetoneAlgMatrixProcessing(;
dn = Denoise(),
alg = LoGo())))]6-element Vector{AbstractPriorEstimator}:
EmpiricalPrior
ce ┼ PortfolioOptimisersCovariance
│ ce ┼ Covariance
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ GeneralCovariance
│ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ w ┴ nothing
│ │ alg ┴ Full()
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ nothing
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
me ┼ SimpleExpectedReturns
│ w ┴ nothing
horizon ┴ nothing
EmpiricalPrior
ce ┼ PortfolioOptimisersCovariance
│ ce ┼ Covariance
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ GeneralCovariance
│ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ w ┴ nothing
│ │ alg ┴ Full()
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ Denoise
│ │ │ alg ┼ FixedDenoise()
│ │ │ args ┼ Tuple{}: ()
│ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ m ┼ Int64: 10
│ │ │ n ┼ Int64: 1000
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
me ┼ ShrunkExpectedReturns
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ ce ┼ PortfolioOptimisersCovariance
│ │ ce ┼ Covariance
│ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ w ┴ nothing
│ │ │ ce ┼ GeneralCovariance
│ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ w ┴ nothing
│ │ │ alg ┴ Full()
│ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ alg ┼ BayesStein
│ │ tgt ┴ VolatilityWeighted()
horizon ┴ nothing
EmpiricalPrior
ce ┼ PortfolioOptimisersCovariance
│ ce ┼ Covariance
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ GeneralCovariance
│ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ w ┴ nothing
│ │ alg ┴ Full()
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ nothing
│ │ dt ┼ nothing
│ │ alg ┼ LoGo
│ │ │ dist ┼ Distance
│ │ │ │ power ┼ nothing
│ │ │ │ alg ┴ CanonicalDistance()
│ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ order ┴ DenoiseDetoneAlg()
me ┼ ShrunkExpectedReturns
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ ce ┼ PortfolioOptimisersCovariance
│ │ ce ┼ Covariance
│ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ w ┴ nothing
│ │ │ ce ┼ GeneralCovariance
│ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ w ┴ nothing
│ │ │ alg ┴ Full()
│ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ alg ┼ BayesStein
│ │ tgt ┴ MeanSquaredError()
horizon ┴ nothing
HighOrderPriorEstimator
pe ┼ EmpiricalPrior
│ ce ┼ PortfolioOptimisersCovariance
│ │ ce ┼ Covariance
│ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ w ┴ nothing
│ │ │ ce ┼ GeneralCovariance
│ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ w ┴ nothing
│ │ │ alg ┴ Full()
│ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ ShrunkDenoise
│ │ │ │ │ alpha ┴ Float64: 0.5
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ me ┼ ShrunkExpectedReturns
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ PortfolioOptimisersCovariance
│ │ │ ce ┼ Covariance
│ │ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ │ w ┴ nothing
│ │ │ │ ce ┼ GeneralCovariance
│ │ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ │ w ┴ nothing
│ │ │ │ alg ┴ Full()
│ │ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ │ dn ┼ nothing
│ │ │ │ dt ┼ nothing
│ │ │ │ alg ┼ nothing
│ │ │ │ order ┴ DenoiseDetoneAlg()
│ │ alg ┼ BodnarOkhrinParolya
│ │ │ tgt ┴ GrandMean()
│ horizon ┴ nothing
kte ┼ Cokurtosis
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ nothing
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()
ske ┼ Coskewness
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ nothing
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()
HighOrderPriorEstimator
pe ┼ EmpiricalPrior
│ ce ┼ PortfolioOptimisersCovariance
│ │ ce ┼ Covariance
│ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ w ┴ nothing
│ │ │ ce ┼ GeneralCovariance
│ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ w ┴ nothing
│ │ │ alg ┴ Full()
│ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ FixedDenoise()
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ LoGo
│ │ │ │ dist ┼ Distance
│ │ │ │ │ power ┼ nothing
│ │ │ │ │ alg ┴ CanonicalDistance()
│ │ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ order ┴ DenoiseDetoneAlg()
│ me ┼ ShrunkExpectedReturns
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ PortfolioOptimisersCovariance
│ │ │ ce ┼ Covariance
│ │ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ │ w ┴ nothing
│ │ │ │ ce ┼ GeneralCovariance
│ │ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ │ w ┴ nothing
│ │ │ │ alg ┴ Full()
│ │ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ │ dn ┼ nothing
│ │ │ │ dt ┼ nothing
│ │ │ │ alg ┼ nothing
│ │ │ │ order ┴ DenoiseDetoneAlg()
│ │ alg ┼ BodnarOkhrinParolya
│ │ │ tgt ┴ VolatilityWeighted()
│ horizon ┴ nothing
kte ┼ Cokurtosis
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ Denoise
│ │ │ alg ┼ FixedDenoise()
│ │ │ args ┼ Tuple{}: ()
│ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ m ┼ Int64: 10
│ │ │ n ┼ Int64: 1000
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()
ske ┼ Coskewness
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ Denoise
│ │ │ alg ┼ FixedDenoise()
│ │ │ args ┼ Tuple{}: ()
│ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ m ┼ Int64: 10
│ │ │ n ┼ Int64: 1000
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dt ┼ nothing
│ │ alg ┼ nothing
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()
HighOrderPriorEstimator
pe ┼ EmpiricalPrior
│ ce ┼ PortfolioOptimisersCovariance
│ │ ce ┼ Covariance
│ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ w ┴ nothing
│ │ │ ce ┼ GeneralCovariance
│ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ w ┴ nothing
│ │ │ alg ┴ Full()
│ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ LoGo
│ │ │ │ dist ┼ Distance
│ │ │ │ │ power ┼ nothing
│ │ │ │ │ alg ┴ CanonicalDistance()
│ │ │ │ sim ┼ ExponentialSimilarity()
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ order ┴ DenoiseDetoneAlg()
│ me ┼ ShrunkExpectedReturns
│ │ me ┼ SimpleExpectedReturns
│ │ │ w ┴ nothing
│ │ ce ┼ PortfolioOptimisersCovariance
│ │ │ ce ┼ Covariance
│ │ │ │ me ┼ SimpleExpectedReturns
│ │ │ │ │ w ┴ nothing
│ │ │ │ ce ┼ GeneralCovariance
│ │ │ │ │ ce ┼ SimpleCovariance: SimpleCovariance(true)
│ │ │ │ │ w ┴ nothing
│ │ │ │ alg ┴ Full()
│ │ │ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ │ dn ┼ nothing
│ │ │ │ dt ┼ nothing
│ │ │ │ alg ┼ nothing
│ │ │ │ order ┴ DenoiseDetoneAlg()
│ │ alg ┼ BodnarOkhrinParolya
│ │ │ tgt ┴ MeanSquaredError()
│ horizon ┴ nothing
kte ┼ Cokurtosis
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ Denoise
│ │ │ alg ┼ ShrunkDenoise
│ │ │ │ alpha ┴ Float64: 0.0
│ │ │ args ┼ Tuple{}: ()
│ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ m ┼ Int64: 10
│ │ │ n ┼ Int64: 1000
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dt ┼ nothing
│ │ alg ┼ LoGo
│ │ │ dist ┼ Distance
│ │ │ │ power ┼ nothing
│ │ │ │ alg ┴ CanonicalDistance()
│ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()
ske ┼ Coskewness
│ me ┼ SimpleExpectedReturns
│ │ w ┴ nothing
│ mp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dn ┼ Denoise
│ │ │ alg ┼ ShrunkDenoise
│ │ │ │ alpha ┴ Float64: 0.0
│ │ │ args ┼ Tuple{}: ()
│ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ m ┼ Int64: 10
│ │ │ n ┼ Int64: 1000
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ dt ┼ nothing
│ │ alg ┼ LoGo
│ │ │ dist ┼ Distance
│ │ │ │ power ┼ nothing
│ │ │ │ alg ┴ CanonicalDistance()
│ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ order ┴ DenoiseDetoneAlg()
│ alg ┴ Full()Now let's compute the prior statistics for each estimator.
prs = prior.(pes, rd)6-element Vector{AbstractPriorResult}:
LowOrderPrior
X ┼ 252×20 Matrix{Float64}
mu ┼ 20-element Vector{Float64}
sigma ┼ 20×20 Matrix{Float64}
chol ┼ nothing
w ┼ nothing
ens ┼ nothing
kld ┼ nothing
ow ┼ nothing
rr ┼ nothing
f_mu ┼ nothing
f_sigma ┼ nothing
f_w ┴ nothing
LowOrderPrior
X ┼ 252×20 Matrix{Float64}
mu ┼ 20-element Vector{Float64}
sigma ┼ 20×20 Matrix{Float64}
chol ┼ nothing
w ┼ nothing
ens ┼ nothing
kld ┼ nothing
ow ┼ nothing
rr ┼ nothing
f_mu ┼ nothing
f_sigma ┼ nothing
f_w ┴ nothing
LowOrderPrior
X ┼ 252×20 Matrix{Float64}
mu ┼ 20-element Vector{Float64}
sigma ┼ 20×20 Matrix{Float64}
chol ┼ nothing
w ┼ nothing
ens ┼ nothing
kld ┼ nothing
ow ┼ nothing
rr ┼ nothing
f_mu ┼ nothing
f_sigma ┼ nothing
f_w ┴ nothing
HighOrderPrior
pr ┼ LowOrderPrior
│ X ┼ 252×20 Matrix{Float64}
│ mu ┼ 20-element Vector{Float64}
│ sigma ┼ 20×20 Matrix{Float64}
│ chol ┼ nothing
│ w ┼ nothing
│ ens ┼ nothing
│ kld ┼ nothing
│ ow ┼ nothing
│ rr ┼ nothing
│ f_mu ┼ nothing
│ f_sigma ┼ nothing
│ f_w ┴ nothing
kt ┼ 400×400 Matrix{Float64}
L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
sk ┼ 20×400 Matrix{Float64}
V ┼ 20×20 Matrix{Float64}
skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ pdm ┼ Posdef
│ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ dn ┼ nothing
│ dt ┼ nothing
│ alg ┼ nothing
│ order ┴ DenoiseDetoneAlg()
f_kt ┼ nothing
f_sk ┼ nothing
f_V ┴ nothing
HighOrderPrior
pr ┼ LowOrderPrior
│ X ┼ 252×20 Matrix{Float64}
│ mu ┼ 20-element Vector{Float64}
│ sigma ┼ 20×20 Matrix{Float64}
│ chol ┼ nothing
│ w ┼ nothing
│ ens ┼ nothing
│ kld ┼ nothing
│ ow ┼ nothing
│ rr ┼ nothing
│ f_mu ┼ nothing
│ f_sigma ┼ nothing
│ f_w ┴ nothing
kt ┼ 400×400 Matrix{Float64}
L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
sk ┼ 20×400 Matrix{Float64}
V ┼ 20×20 Matrix{Float64}
skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ pdm ┼ Posdef
│ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ dn ┼ Denoise
│ │ alg ┼ FixedDenoise()
│ │ args ┼ Tuple{}: ()
│ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ m ┼ Int64: 10
│ │ n ┼ Int64: 1000
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ dt ┼ nothing
│ alg ┼ nothing
│ order ┴ DenoiseDetoneAlg()
f_kt ┼ nothing
f_sk ┼ nothing
f_V ┴ nothing
HighOrderPrior
pr ┼ LowOrderPrior
│ X ┼ 252×20 Matrix{Float64}
│ mu ┼ 20-element Vector{Float64}
│ sigma ┼ 20×20 Matrix{Float64}
│ chol ┼ nothing
│ w ┼ nothing
│ ens ┼ nothing
│ kld ┼ nothing
│ ow ┼ nothing
│ rr ┼ nothing
│ f_mu ┼ nothing
│ f_sigma ┼ nothing
│ f_w ┴ nothing
kt ┼ 400×400 Matrix{Float64}
L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
sk ┼ 20×400 Matrix{Float64}
V ┼ 20×20 Matrix{Float64}
skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ pdm ┼ Posdef
│ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ dn ┼ Denoise
│ │ alg ┼ ShrunkDenoise
│ │ │ alpha ┴ Float64: 0.0
│ │ args ┼ Tuple{}: ()
│ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ m ┼ Int64: 10
│ │ n ┼ Int64: 1000
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ dt ┼ nothing
│ alg ┼ LoGo
│ │ dist ┼ Distance
│ │ │ power ┼ nothing
│ │ │ alg ┴ CanonicalDistance()
│ │ sim ┼ MaximumDistanceSimilarity()
│ │ pdm ┼ Posdef
│ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ order ┴ DenoiseDetoneAlg()
f_kt ┼ nothing
f_sk ┼ nothing
f_V ┴ nothing2.1 Expected returns
First let's view the expected returns.
pretty_table(DataFrame("Assets" => rd.nx, "Vanilla" => prs[1].mu, "BS(VW)" => prs[2].mu,
"BS(MSE)" => prs[3].mu, "BOP(GM)" => prs[4].mu,
"BOP(VW)" => prs[5].mu, "BOP(MSE)" => prs[6].mu);
formatters = [mmtfmt], title = "Expected returns") Expected returns
┌────────┬──────────┬──────────┬──────────┬──────────┬──────────┬──────────┐
│ Assets │ Vanilla │ BS(VW) │ BS(MSE) │ BOP(GM) │ BOP(VW) │ BOP(MSE) │
│ String │ Float64 │ Float64 │ Float64 │ Float64 │ Float64 │ Float64 │
├────────┼──────────┼──────────┼──────────┼──────────┼──────────┼──────────┤
│ AAPL │ -0.113 % │ 0.009 % │ -0.045 % │ 0.064 % │ 0.082 % │ 0.063 % │
│ AMD │ -0.281 % │ -0.056 % │ -0.116 % │ 0.158 % │ 0.176 % │ 0.157 % │
│ BAC │ -0.093 % │ 0.016 % │ -0.037 % │ 0.053 % │ 0.071 % │ 0.052 % │
│ BBY │ -0.028 % │ 0.042 % │ -0.01 % │ 0.016 % │ 0.034 % │ 0.016 % │
│ CVX │ 0.195 % │ 0.128 % │ 0.084 % │ -0.108 % │ -0.09 % │ -0.109 % │
│ GE │ -0.034 % │ 0.039 % │ -0.012 % │ 0.02 % │ 0.038 % │ 0.019 % │
│ HD │ -0.071 % │ 0.025 % │ -0.028 % │ 0.04 % │ 0.058 % │ 0.04 % │
│ JNJ │ 0.031 % │ 0.064 % │ 0.015 % │ -0.017 % │ 0.001 % │ -0.017 % │
│ JPM │ -0.042 % │ 0.036 % │ -0.015 % │ 0.024 % │ 0.042 % │ 0.023 % │
│ KO │ 0.05 % │ 0.072 % │ 0.023 % │ -0.027 % │ -0.009 % │ -0.028 % │
│ LLY │ 0.131 % │ 0.103 % │ 0.057 % │ -0.073 % │ -0.055 % │ -0.073 % │
│ MRK │ 0.167 % │ 0.117 % │ 0.072 % │ -0.093 % │ -0.075 % │ -0.093 % │
│ MSFT │ -0.121 % │ 0.006 % │ -0.049 % │ 0.068 % │ 0.086 % │ 0.068 % │
│ PEP │ 0.039 % │ 0.068 % │ 0.019 % │ -0.021 % │ -0.003 % │ -0.022 % │
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │
└────────┴──────────┴──────────┴──────────┴──────────┴──────────┴──────────┘
6 rows omitted2.2 Covariance matrices
We can now see how the different denoising and sparsification techniques improve the covariance matrix's condition number.
using LinearAlgebra
pretty_table(DataFrame([rd.nx prs[1].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: Vanilla",
source_notes = "Condition number Vanilla: $(round(cond(prs[1].sigma); digits = 3))")
pretty_table(DataFrame([rd.nx prs[2].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: Fixed denoise",
source_notes = "Condition number fixed denoise: $(round(cond(prs[2].sigma); digits = 3))")
pretty_table(DataFrame([rd.nx prs[3].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: LoGo(MaxDist)",
source_notes = "Condition number LoGo(MaxDist): $(round(cond(prs[3].sigma); digits = 3))")
pretty_table(DataFrame([rd.nx prs[4].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: Shrunk denoise (0.5)",
source_notes = "Condition number Shrunk denoise (0.5): $(round(cond(prs[4].sigma); digits = 3))")
pretty_table(DataFrame([rd.nx prs[5].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: FixedDenoise + LoGo(MaxDist)",
source_notes = "Condition number FixedDenoise + LoGo(MaxDist): $(round(cond(prs[5].sigma); digits = 3))")
pretty_table(DataFrame([rd.nx prs[6].sigma], ["Assets"; rd.nx]); formatters = [mmtfmt],
title = "Covariance: LoGo(ExpDist)",
source_notes = "Condition number LoGo(ExpDist): $(round(cond(prs[6].sigma); digits = 3))") Covariance: Vanilla
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.063 % │ 0.026 % │ 0.034 % │ 0.014 % │ 0.027 % │ 0.026 % ⋯
│ AMD │ 0.063 % │ 0.147 % │ 0.044 % │ 0.057 % │ 0.025 % │ 0.049 % │ 0.039 % ⋯
│ BAC │ 0.026 % │ 0.044 % │ 0.042 % │ 0.026 % │ 0.015 % │ 0.028 % │ 0.017 % ⋯
│ BBY │ 0.034 % │ 0.057 % │ 0.026 % │ 0.081 % │ 0.013 % │ 0.027 % │ 0.037 % ⋯
│ CVX │ 0.014 % │ 0.025 % │ 0.015 % │ 0.013 % │ 0.043 % │ 0.017 % │ 0.007 % ⋯
│ GE │ 0.027 % │ 0.049 % │ 0.028 % │ 0.027 % │ 0.017 % │ 0.048 % │ 0.017 % ⋯
│ HD │ 0.026 % │ 0.039 % │ 0.017 % │ 0.037 % │ 0.007 % │ 0.017 % │ 0.039 % ⋯
│ JNJ │ 0.009 % │ 0.008 % │ 0.007 % │ 0.009 % │ 0.003 % │ 0.006 % │ 0.008 % ⋯
│ JPM │ 0.023 % │ 0.037 % │ 0.034 % │ 0.025 % │ 0.012 % │ 0.025 % │ 0.018 % ⋯
│ KO │ 0.014 % │ 0.017 % │ 0.011 % │ 0.014 % │ 0.005 % │ 0.011 % │ 0.012 % ⋯
│ LLY │ 0.014 % │ 0.018 % │ 0.009 % │ 0.012 % │ 0.007 % │ 0.011 % │ 0.013 % ⋯
│ MRK │ 0.008 % │ 0.005 % │ 0.007 % │ 0.005 % │ 0.005 % │ 0.006 % │ 0.006 % ⋯
│ MSFT │ 0.041 % │ 0.061 % │ 0.025 % │ 0.032 % │ 0.012 % │ 0.023 % │ 0.027 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number Vanilla: 177.279
Covariance: Fixed denoise
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.052 % │ 0.027 % │ 0.037 % │ 0.013 % │ 0.028 % │ 0.026 % ⋯
│ AMD │ 0.052 % │ 0.147 % │ 0.047 % │ 0.06 % │ 0.022 % │ 0.049 % │ 0.04 % ⋯
│ BAC │ 0.027 % │ 0.047 % │ 0.042 % │ 0.028 % │ 0.014 % │ 0.027 % │ 0.02 % ⋯
│ BBY │ 0.037 % │ 0.06 % │ 0.028 % │ 0.081 % │ 0.012 % │ 0.029 % │ 0.032 % ⋯
│ CVX │ 0.013 % │ 0.022 % │ 0.014 % │ 0.012 % │ 0.043 % │ 0.017 % │ 0.007 % ⋯
│ GE │ 0.028 % │ 0.049 % │ 0.027 % │ 0.029 % │ 0.017 % │ 0.048 % │ 0.02 % ⋯
│ HD │ 0.026 % │ 0.04 % │ 0.02 % │ 0.032 % │ 0.007 % │ 0.02 % │ 0.039 % ⋯
│ JNJ │ 0.008 % │ 0.008 % │ 0.006 % │ 0.007 % │ 0.002 % │ 0.006 % │ 0.008 % ⋯
│ JPM │ 0.025 % │ 0.043 % │ 0.024 % │ 0.026 % │ 0.011 % │ 0.025 % │ 0.018 % ⋯
│ KO │ 0.014 % │ 0.017 % │ 0.01 % │ 0.016 % │ 0.004 % │ 0.01 % │ 0.013 % ⋯
│ LLY │ 0.014 % │ 0.015 % │ 0.012 % │ 0.011 % │ 0.007 % │ 0.012 % │ 0.011 % ⋯
│ MRK │ 0.007 % │ 0.006 % │ 0.006 % │ 0.004 % │ 0.005 % │ 0.006 % │ 0.006 % ⋯
│ MSFT │ 0.031 % │ 0.051 % │ 0.027 % │ 0.036 % │ 0.011 % │ 0.027 % │ 0.026 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number fixed denoise: 87.203
Covariance: LoGo(MaxDist)
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.063 % │ 0.026 % │ 0.034 % │ 0.013 % │ 0.027 % │ 0.026 % ⋯
│ AMD │ 0.063 % │ 0.147 % │ 0.044 % │ 0.057 % │ 0.025 % │ 0.049 % │ 0.039 % ⋯
│ BAC │ 0.026 % │ 0.044 % │ 0.042 % │ 0.022 % │ 0.015 % │ 0.028 % │ 0.015 % ⋯
│ BBY │ 0.034 % │ 0.057 % │ 0.022 % │ 0.081 % │ 0.012 % │ 0.027 % │ 0.037 % ⋯
│ CVX │ 0.013 % │ 0.025 % │ 0.015 % │ 0.012 % │ 0.043 % │ 0.017 % │ 0.008 % ⋯
│ GE │ 0.027 % │ 0.049 % │ 0.028 % │ 0.027 % │ 0.017 % │ 0.048 % │ 0.017 % ⋯
│ HD │ 0.026 % │ 0.039 % │ 0.015 % │ 0.037 % │ 0.008 % │ 0.017 % │ 0.039 % ⋯
│ JNJ │ 0.009 % │ 0.01 % │ 0.004 % │ 0.006 % │ 0.002 % │ 0.005 % │ 0.005 % ⋯
│ JPM │ 0.023 % │ 0.039 % │ 0.034 % │ 0.02 % │ 0.013 % │ 0.025 % │ 0.014 % ⋯
│ KO │ 0.014 % │ 0.017 % │ 0.007 % │ 0.01 % │ 0.004 % │ 0.008 % │ 0.008 % ⋯
│ LLY │ 0.011 % │ 0.013 % │ 0.005 % │ 0.007 % │ 0.003 % │ 0.006 % │ 0.006 % ⋯
│ MRK │ 0.007 % │ 0.009 % │ 0.004 % │ 0.005 % │ 0.002 % │ 0.004 % │ 0.004 % ⋯
│ MSFT │ 0.041 % │ 0.061 % │ 0.023 % │ 0.033 % │ 0.012 % │ 0.025 % │ 0.027 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number LoGo(MaxDist): 157.814
Covariance: Shrunk denoise (0.5)
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.061 % │ 0.028 % │ 0.037 % │ 0.014 % │ 0.028 % │ 0.027 % ⋯
│ AMD │ 0.061 % │ 0.147 % │ 0.049 % │ 0.06 % │ 0.024 % │ 0.051 % │ 0.041 % ⋯
│ BAC │ 0.028 % │ 0.049 % │ 0.042 % │ 0.027 % │ 0.015 % │ 0.029 % │ 0.019 % ⋯
│ BBY │ 0.037 % │ 0.06 % │ 0.027 % │ 0.081 % │ 0.012 % │ 0.028 % │ 0.035 % ⋯
│ CVX │ 0.014 % │ 0.024 % │ 0.015 % │ 0.012 % │ 0.043 % │ 0.018 % │ 0.007 % ⋯
│ GE │ 0.028 % │ 0.051 % │ 0.029 % │ 0.028 % │ 0.018 % │ 0.048 % │ 0.018 % ⋯
│ HD │ 0.027 % │ 0.041 % │ 0.019 % │ 0.035 % │ 0.007 % │ 0.018 % │ 0.039 % ⋯
│ JNJ │ 0.009 % │ 0.008 % │ 0.007 % │ 0.008 % │ 0.002 % │ 0.006 % │ 0.008 % ⋯
│ JPM │ 0.026 % │ 0.043 % │ 0.031 % │ 0.026 % │ 0.012 % │ 0.026 % │ 0.018 % ⋯
│ KO │ 0.015 % │ 0.017 % │ 0.01 % │ 0.016 % │ 0.005 % │ 0.01 % │ 0.013 % ⋯
│ LLY │ 0.014 % │ 0.016 % │ 0.011 % │ 0.011 % │ 0.007 % │ 0.011 % │ 0.011 % ⋯
│ MRK │ 0.007 % │ 0.005 % │ 0.007 % │ 0.004 % │ 0.005 % │ 0.006 % │ 0.006 % ⋯
│ MSFT │ 0.038 % │ 0.06 % │ 0.027 % │ 0.035 % │ 0.012 % │ 0.026 % │ 0.027 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number Shrunk denoise (0.5): 135.392
Covariance: FixedDenoise + LoGo(MaxDist)
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.052 % │ 0.027 % │ 0.037 % │ 0.013 % │ 0.028 % │ 0.026 % ⋯
│ AMD │ 0.052 % │ 0.147 % │ 0.047 % │ 0.06 % │ 0.018 % │ 0.038 % │ 0.04 % ⋯
│ BAC │ 0.027 % │ 0.047 % │ 0.042 % │ 0.025 % │ 0.014 % │ 0.027 % │ 0.018 % ⋯
│ BBY │ 0.037 % │ 0.06 % │ 0.025 % │ 0.081 % │ 0.011 % │ 0.023 % │ 0.032 % ⋯
│ CVX │ 0.013 % │ 0.018 % │ 0.014 % │ 0.011 % │ 0.043 % │ 0.017 % │ 0.008 % ⋯
│ GE │ 0.028 % │ 0.038 % │ 0.027 % │ 0.023 % │ 0.017 % │ 0.048 % │ 0.017 % ⋯
│ HD │ 0.026 % │ 0.04 % │ 0.018 % │ 0.032 % │ 0.008 % │ 0.017 % │ 0.039 % ⋯
│ JNJ │ 0.008 % │ 0.011 % │ 0.005 % │ 0.008 % │ 0.002 % │ 0.005 % │ 0.008 % ⋯
│ JPM │ 0.025 % │ 0.036 % │ 0.024 % │ 0.021 % │ 0.011 % │ 0.025 % │ 0.016 % ⋯
│ KO │ 0.014 % │ 0.019 % │ 0.009 % │ 0.014 % │ 0.004 % │ 0.009 % │ 0.013 % ⋯
│ LLY │ 0.011 % │ 0.015 % │ 0.007 % │ 0.011 % │ 0.003 % │ 0.007 % │ 0.011 % ⋯
│ MRK │ 0.007 % │ 0.01 % │ 0.005 % │ 0.007 % │ 0.002 % │ 0.005 % │ 0.007 % ⋯
│ MSFT │ 0.031 % │ 0.051 % │ 0.027 % │ 0.03 % │ 0.011 % │ 0.023 % │ 0.026 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number FixedDenoise + LoGo(MaxDist): 86.573
Covariance: LoGo(ExpDist)
┌────────┬─────────┬─────────┬─────────┬─────────┬─────────┬─────────┬──────────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ GE │ HD ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ Any │ Any ⋯
├────────┼─────────┼─────────┼─────────┼─────────┼─────────┼─────────┼──────────
│ AAPL │ 0.05 % │ 0.063 % │ 0.026 % │ 0.034 % │ 0.013 % │ 0.027 % │ 0.026 % ⋯
│ AMD │ 0.063 % │ 0.147 % │ 0.044 % │ 0.057 % │ 0.025 % │ 0.049 % │ 0.039 % ⋯
│ BAC │ 0.026 % │ 0.044 % │ 0.042 % │ 0.022 % │ 0.015 % │ 0.028 % │ 0.015 % ⋯
│ BBY │ 0.034 % │ 0.057 % │ 0.022 % │ 0.081 % │ 0.012 % │ 0.027 % │ 0.037 % ⋯
│ CVX │ 0.013 % │ 0.025 % │ 0.015 % │ 0.012 % │ 0.043 % │ 0.017 % │ 0.008 % ⋯
│ GE │ 0.027 % │ 0.049 % │ 0.028 % │ 0.027 % │ 0.017 % │ 0.048 % │ 0.017 % ⋯
│ HD │ 0.026 % │ 0.039 % │ 0.015 % │ 0.037 % │ 0.008 % │ 0.017 % │ 0.039 % ⋯
│ JNJ │ 0.009 % │ 0.011 % │ 0.004 % │ 0.006 % │ 0.002 % │ 0.005 % │ 0.005 % ⋯
│ JPM │ 0.023 % │ 0.039 % │ 0.034 % │ 0.02 % │ 0.013 % │ 0.025 % │ 0.014 % ⋯
│ KO │ 0.014 % │ 0.018 % │ 0.008 % │ 0.01 % │ 0.004 % │ 0.008 % │ 0.008 % ⋯
│ LLY │ 0.01 % │ 0.013 % │ 0.005 % │ 0.007 % │ 0.003 % │ 0.006 % │ 0.006 % ⋯
│ MRK │ 0.007 % │ 0.009 % │ 0.004 % │ 0.005 % │ 0.002 % │ 0.004 % │ 0.004 % ⋯
│ MSFT │ 0.041 % │ 0.061 % │ 0.023 % │ 0.033 % │ 0.012 % │ 0.025 % │ 0.027 % ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ ⋱
└────────┴─────────┴─────────┴─────────┴─────────┴─────────┴─────────┴──────────
13 columns and 7 rows omitted
Condition number LoGo(ExpDist): 159.8462.3 Higher order moments
Now let's view how the higher order moments benefit from denoising. The coskewness matrix is not affected because it's not square, but the matrix of negative spectral slices is.
nx2 = collect(Iterators.flatten([(nx * "_") .* rd.nx for nx in rd.nx]))
pretty_table(DataFrame([rd.nx prs[4].V], ["Assets"; rd.nx]); formatters = [hmmtfmt],
title = "Coskewness Negative Spectral Slices: Vanilla",
source_notes = "Condition number Vanilla: $(round(cond(prs[4].V); digits = 3))")
pretty_table(DataFrame([rd.nx prs[5].V], ["Assets"; rd.nx]); formatters = [hmmtfmt],
title = "Coskewness Negative Spectral Slices: FixedDenoise",
source_notes = "Condition number FixedDenoise: $(round(cond(prs[5].V); digits = 3))")
pretty_table(DataFrame([rd.nx prs[6].V], ["Assets"; rd.nx]); formatters = [hmmtfmt],
title = "Coskewness Negative Spectral Slices: LoGo(MaxDist)",
source_notes = "Condition number LoGo(MaxDist): $(round(cond(prs[6].V); digits = 3))") Coskewness Negative Spectral Slices: Vanilla
┌────────┬────────────┬────────────┬────────────┬────────────┬────────────┬─────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├────────┼────────────┼────────────┼────────────┼────────────┼────────────┼─────
│ AAPL │ 10.95e-4 % │ 8.74e-4 % │ 0.42e-4 % │ 11.72e-4 % │ 6.82e-4 % │ 8 ⋯
│ AMD │ 8.74e-4 % │ 39.47e-4 % │ 3.05e-4 % │ 10.18e-4 % │ 16.53e-4 % │ 23 ⋯
│ BAC │ 0.42e-4 % │ 3.05e-4 % │ 4.83e-4 % │ 3.92e-4 % │ -0.99e-4 % │ 0 ⋯
│ BBY │ 11.72e-4 % │ 10.18e-4 % │ 3.92e-4 % │ 44.51e-4 % │ 3.51e-4 % │ 6 ⋯
│ CVX │ 6.82e-4 % │ 16.53e-4 % │ -0.99e-4 % │ 3.51e-4 % │ 31.05e-4 % │ 14 ⋯
│ GE │ 8.11e-4 % │ 23.22e-4 % │ 0.02e-4 % │ 6.39e-4 % │ 14.81e-4 % │ 37 ⋯
│ HD │ 8.11e-4 % │ 1.1e-4 % │ 2.36e-4 % │ 21.55e-4 % │ -1.51e-4 % │ 1 ⋯
│ JNJ │ 2.67e-4 % │ 0.82e-4 % │ -0.36e-4 % │ 5.79e-4 % │ 1.36e-4 % │ -0 ⋯
│ JPM │ -1.57e-4 % │ -2.69e-4 % │ 2.12e-4 % │ -2.19e-4 % │ -5.87e-4 % │ -2 ⋯
│ KO │ 5.55e-4 % │ 1.42e-4 % │ 1.57e-4 % │ 15.44e-4 % │ 2.42e-4 % │ 3 ⋯
│ LLY │ 3.15e-4 % │ 5.99e-4 % │ 0.52e-4 % │ 7.1e-4 % │ 3.94e-4 % │ 5 ⋯
│ MRK │ 1.39e-4 % │ 0.44e-4 % │ 0.02e-4 % │ 0.1e-4 % │ 2.34e-4 % │ 4 ⋯
│ MSFT │ 7.36e-4 % │ 13.13e-4 % │ 0.08e-4 % │ 8.4e-4 % │ 6.19e-4 % │ 10 ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴────────────┴────────────┴────────────┴────────────┴────────────┴─────
15 columns and 7 rows omitted
Condition number Vanilla: 129.142
Coskewness Negative Spectral Slices: FixedDenoise
┌────────┬────────────┬────────────┬────────────┬────────────┬────────────┬─────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├────────┼────────────┼────────────┼────────────┼────────────┼────────────┼─────
│ AAPL │ 10.95e-4 % │ 9.57e-4 % │ 0.69e-4 % │ 11.57e-4 % │ 6.33e-4 % │ 8 ⋯
│ AMD │ 9.57e-4 % │ 39.47e-4 % │ 2.5e-4 % │ 9.59e-4 % │ 16.04e-4 % │ 22 ⋯
│ BAC │ 0.69e-4 % │ 2.5e-4 % │ 4.83e-4 % │ 3.11e-4 % │ -1.68e-4 % │ 1 ⋯
│ BBY │ 11.57e-4 % │ 9.59e-4 % │ 3.11e-4 % │ 44.51e-4 % │ 2.12e-4 % │ 7 ⋯
│ CVX │ 6.33e-4 % │ 16.04e-4 % │ -1.68e-4 % │ 2.12e-4 % │ 31.05e-4 % │ 17 ⋯
│ GE │ 8.54e-4 % │ 22.19e-4 % │ 1.62e-4 % │ 7.31e-4 % │ 17.18e-4 % │ 37 ⋯
│ HD │ 6.9e-4 % │ 5.01e-4 % │ 2.65e-4 % │ 19.02e-4 % │ -2.4e-4 % │ 3 ⋯
│ JNJ │ 2.49e-4 % │ 0.49e-4 % │ -0.44e-4 % │ 5.99e-4 % │ 0.82e-4 % │ 1 ⋯
│ JPM │ -2.17e-4 % │ -2.21e-4 % │ 2.63e-4 % │ -1.37e-4 % │ -5.38e-4 % │ -2 ⋯
│ KO │ 4.58e-4 % │ 1.53e-4 % │ 1.64e-4 % │ 13.45e-4 % │ 2.85e-4 % │ 1 ⋯
│ LLY │ 3.83e-4 % │ 6.23e-4 % │ 0.29e-4 % │ 5.94e-4 % │ 3.98e-4 % │ 6 ⋯
│ MRK │ 0.79e-4 % │ 1.38e-4 % │ -0.1e-4 % │ 0.39e-4 % │ 2.9e-4 % │ 3 ⋯
│ MSFT │ 6.05e-4 % │ 11.6e-4 % │ 0.45e-4 % │ 8.37e-4 % │ 6.82e-4 % │ 10 ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴────────────┴────────────┴────────────┴────────────┴────────────┴─────
15 columns and 7 rows omitted
Condition number FixedDenoise: 67.939
Coskewness Negative Spectral Slices: LoGo(MaxDist)
┌────────┬────────────┬────────────┬───────────┬────────────┬────────────┬──────
│ Assets │ AAPL │ AMD │ BAC │ BBY │ CVX │ ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├────────┼────────────┼────────────┼───────────┼────────────┼────────────┼──────
│ AAPL │ 10.95e-4 % │ 10.51e-4 % │ 1.06e-4 % │ 13.13e-4 % │ 5.88e-4 % │ 8. ⋯
│ AMD │ 10.51e-4 % │ 39.47e-4 % │ 1.27e-4 % │ 15.19e-4 % │ 18.74e-4 % │ 24. ⋯
│ BAC │ 1.06e-4 % │ 1.27e-4 % │ 4.83e-4 % │ 3.39e-4 % │ 0.7e-4 % │ 1 ⋯
│ BBY │ 13.13e-4 % │ 15.19e-4 % │ 3.39e-4 % │ 44.51e-4 % │ 8.46e-4 % │ 12. ⋯
│ CVX │ 5.88e-4 % │ 18.74e-4 % │ 0.7e-4 % │ 8.46e-4 % │ 31.05e-4 % │ 18. ⋯
│ GE │ 8.52e-4 % │ 24.43e-4 % │ 1.0e-4 % │ 12.13e-4 % │ 18.85e-4 % │ 37. ⋯
│ HD │ 7.2e-4 % │ 8.17e-4 % │ 1.72e-4 % │ 21.68e-4 % │ 4.54e-4 % │ 6. ⋯
│ JNJ │ 2.51e-4 % │ 3.92e-4 % │ 0.44e-4 % │ 4.63e-4 % │ 2.15e-4 % │ 3. ⋯
│ JPM │ 0.24e-4 % │ 0.27e-4 % │ 3.28e-4 % │ 0.9e-4 % │ 0.15e-4 % │ 0. ⋯
│ KO │ 5.44e-4 % │ 6.75e-4 % │ 1.93e-4 % │ 16.13e-4 % │ 3.7e-4 % │ 5. ⋯
│ LLY │ 3.37e-4 % │ 5.88e-4 % │ 0.52e-4 % │ 5.8e-4 % │ 3.28e-4 % │ 4. ⋯
│ MRK │ 2.09e-4 % │ 3.13e-4 % │ 0.38e-4 % │ 3.91e-4 % │ 1.71e-4 % │ 2 ⋯
│ MSFT │ 6.83e-4 % │ 13.81e-4 % │ 0.83e-4 % │ 10.15e-4 % │ 7.82e-4 % │ 11. ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴────────────┴────────────┴───────────┴────────────┴────────────┴──────
15 columns and 7 rows omitted
Condition number LoGo(MaxDist): 86.422And finally the cokurtosis.
pretty_table(DataFrame([nx2 prs[4].kt], ["Assets^2"; nx2]); formatters = [hmmtfmt],
title = "Cokurtosis: Vanilla",
source_notes = "Condition number Vanilla: $(round(cond(prs[4].kt); digits = 3))")
pretty_table(DataFrame([nx2 prs[5].kt], ["Assets^2"; nx2]); formatters = [hmmtfmt],
title = "Cokurtosis: FixedDenoise",
source_notes = "Condition number FixedDenoise: $(round(cond(prs[5].kt); digits = 3))")
pretty_table(DataFrame([nx2 prs[6].kt], ["Assets^2"; nx2]); formatters = [hmmtfmt],
title = "Cokurtosis: Shrunk denoise (0) + LoGo(MaxDist)",
source_notes = "Condition number Shrunk denoise (0) + LoGo(MaxDist): $(round(cond(prs[6].kt); digits = 3))") Cokurtosis: Vanilla
┌───────────┬───────────┬───────────┬───────────┬───────────┬───────────┬───────
│ Assets^2 │ AAPL_AAPL │ AAPL_AMD │ AAPL_BAC │ AAPL_BBY │ AAPL_CVX │ AA ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├───────────┼───────────┼───────────┼───────────┼───────────┼───────────┼───────
│ AAPL_AAPL │ 1.01e-4 % │ 1.17e-4 % │ 0.45e-4 % │ 0.67e-4 % │ 0.19e-4 % │ 0.46 ⋯
│ AAPL_AMD │ 1.17e-4 % │ 1.85e-4 % │ 0.61e-4 % │ 0.88e-4 % │ 0.35e-4 % │ 0.64 ⋯
│ AAPL_BAC │ 0.45e-4 % │ 0.61e-4 % │ 0.35e-4 % │ 0.33e-4 % │ 0.15e-4 % │ 0.27 ⋯
│ AAPL_BBY │ 0.67e-4 % │ 0.88e-4 % │ 0.33e-4 % │ 0.7e-4 % │ 0.17e-4 % │ 0.34 ⋯
│ AAPL_CVX │ 0.19e-4 % │ 0.35e-4 % │ 0.15e-4 % │ 0.17e-4 % │ 0.3e-4 % │ 0.16 ⋯
│ AAPL_GE │ 0.46e-4 % │ 0.64e-4 % │ 0.27e-4 % │ 0.34e-4 % │ 0.16e-4 % │ 0.41 ⋯
│ AAPL_HD │ 0.65e-4 % │ 0.86e-4 % │ 0.31e-4 % │ 0.53e-4 % │ 0.13e-4 % │ 0.3 ⋯
│ AAPL_JNJ │ 0.19e-4 % │ 0.22e-4 % │ 0.1e-4 % │ 0.15e-4 % │ 0.05e-4 % │ 0.1 ⋯
│ AAPL_JPM │ 0.41e-4 % │ 0.57e-4 % │ 0.3e-4 % │ 0.31e-4 % │ 0.13e-4 % │ 0.27 ⋯
│ AAPL_KO │ 0.35e-4 % │ 0.43e-4 % │ 0.18e-4 % │ 0.29e-4 % │ 0.09e-4 % │ 0.17 ⋯
│ AAPL_LLY │ 0.26e-4 % │ 0.34e-4 % │ 0.14e-4 % │ 0.19e-4 % │ 0.07e-4 % │ 0.16 ⋯
│ AAPL_MRK │ 0.13e-4 % │ 0.15e-4 % │ 0.08e-4 % │ 0.08e-4 % │ 0.06e-4 % │ 0.08 ⋯
│ AAPL_MSFT │ 0.78e-4 % │ 1.01e-4 % │ 0.39e-4 % │ 0.56e-4 % │ 0.18e-4 % │ 0.37 ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└───────────┴───────────┴───────────┴───────────┴───────────┴───────────┴───────
395 columns and 387 rows omitted
Condition number Vanilla: 1.876716278891544e15
Cokurtosis: FixedDenoise
┌───────────┬───────────┬───────────┬───────────┬───────────┬───────────┬───────
│ Assets^2 │ AAPL_AAPL │ AAPL_AMD │ AAPL_BAC │ AAPL_BBY │ AAPL_CVX │ AA ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├───────────┼───────────┼───────────┼───────────┼───────────┼───────────┼───────
│ AAPL_AAPL │ 1.01e-4 % │ 1.12e-4 % │ 0.44e-4 % │ 0.66e-4 % │ 0.21e-4 % │ 0.43 ⋯
│ AAPL_AMD │ 1.12e-4 % │ 1.85e-4 % │ 0.59e-4 % │ 0.84e-4 % │ 0.34e-4 % │ 0.6 ⋯
│ AAPL_BAC │ 0.44e-4 % │ 0.59e-4 % │ 0.35e-4 % │ 0.32e-4 % │ 0.15e-4 % │ 0.26 ⋯
│ AAPL_BBY │ 0.66e-4 % │ 0.84e-4 % │ 0.32e-4 % │ 0.7e-4 % │ 0.16e-4 % │ 0.32 ⋯
│ AAPL_CVX │ 0.21e-4 % │ 0.34e-4 % │ 0.15e-4 % │ 0.16e-4 % │ 0.3e-4 % │ 0.16 ⋯
│ AAPL_GE │ 0.43e-4 % │ 0.6e-4 % │ 0.26e-4 % │ 0.32e-4 % │ 0.16e-4 % │ 0.41 ⋯
│ AAPL_HD │ 0.62e-4 % │ 0.82e-4 % │ 0.29e-4 % │ 0.51e-4 % │ 0.13e-4 % │ 0.29 ⋯
│ AAPL_JNJ │ 0.19e-4 % │ 0.21e-4 % │ 0.1e-4 % │ 0.15e-4 % │ 0.04e-4 % │ 0.09 ⋯
│ AAPL_JPM │ 0.41e-4 % │ 0.54e-4 % │ 0.28e-4 % │ 0.3e-4 % │ 0.13e-4 % │ 0.25 ⋯
│ AAPL_KO │ 0.34e-4 % │ 0.41e-4 % │ 0.17e-4 % │ 0.28e-4 % │ 0.09e-4 % │ 0.16 ⋯
│ AAPL_LLY │ 0.28e-4 % │ 0.34e-4 % │ 0.14e-4 % │ 0.19e-4 % │ 0.07e-4 % │ 0.17 ⋯
│ AAPL_MRK │ 0.13e-4 % │ 0.15e-4 % │ 0.08e-4 % │ 0.08e-4 % │ 0.06e-4 % │ 0.08 ⋯
│ AAPL_MSFT │ 0.73e-4 % │ 0.96e-4 % │ 0.38e-4 % │ 0.55e-4 % │ 0.18e-4 % │ 0.36 ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└───────────┴───────────┴───────────┴───────────┴───────────┴───────────┴───────
395 columns and 387 rows omitted
Condition number FixedDenoise: 18069.363
Cokurtosis: Shrunk denoise (0) + LoGo(MaxDist)
┌───────────┬───────────┬───────────┬───────────┬───────────┬───────────┬───────
│ Assets^2 │ AAPL_AAPL │ AAPL_AMD │ AAPL_BAC │ AAPL_BBY │ AAPL_CVX │ AA ⋯
│ Any │ Any │ Any │ Any │ Any │ Any │ ⋯
├───────────┼───────────┼───────────┼───────────┼───────────┼───────────┼───────
│ AAPL_AAPL │ 1.01e-4 % │ 1.13e-4 % │ 0.44e-4 % │ 0.64e-4 % │ 0.02e-4 % │ 0.27 ⋯
│ AAPL_AMD │ 1.13e-4 % │ 1.85e-4 % │ 0.61e-4 % │ 0.86e-4 % │ 0.03e-4 % │ 0.37 ⋯
│ AAPL_BAC │ 0.44e-4 % │ 0.61e-4 % │ 0.35e-4 % │ 0.33e-4 % │ 0.01e-4 % │ 0.21 ⋯
│ AAPL_BBY │ 0.64e-4 % │ 0.86e-4 % │ 0.33e-4 % │ 0.7e-4 % │ 0.02e-4 % │ 0.2 ⋯
│ AAPL_CVX │ 0.02e-4 % │ 0.03e-4 % │ 0.01e-4 % │ 0.02e-4 % │ 0.3e-4 % │ 0.01 ⋯
│ AAPL_GE │ 0.27e-4 % │ 0.37e-4 % │ 0.21e-4 % │ 0.2e-4 % │ 0.01e-4 % │ 0.41 ⋯
│ AAPL_HD │ 0.64e-4 % │ 0.85e-4 % │ 0.32e-4 % │ 0.52e-4 % │ 0.02e-4 % │ 0.2 ⋯
│ AAPL_JNJ │ 0.12e-4 % │ 0.17e-4 % │ 0.06e-4 % │ 0.1e-4 % │ 0.01e-4 % │ 0.04 ⋯
│ AAPL_JPM │ 0.41e-4 % │ 0.56e-4 % │ 0.3e-4 % │ 0.3e-4 % │ 0.01e-4 % │ 0.18 ⋯
│ AAPL_KO │ 0.27e-4 % │ 0.37e-4 % │ 0.14e-4 % │ 0.23e-4 % │ 0.02e-4 % │ 0.08 ⋯
│ AAPL_LLY │ 0.14e-4 % │ 0.19e-4 % │ 0.07e-4 % │ 0.11e-4 % │ 0.01e-4 % │ 0.04 ⋯
│ AAPL_MRK │ 0.05e-4 % │ 0.07e-4 % │ 0.03e-4 % │ 0.04e-4 % │ 0.02e-4 % │ 0.02 ⋯
│ AAPL_MSFT │ 0.75e-4 % │ 1.01e-4 % │ 0.4e-4 % │ 0.55e-4 % │ 0.02e-4 % │ 0.24 ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└───────────┴───────────┴───────────┴───────────┴───────────┴───────────┴───────
395 columns and 387 rows omitted
Condition number Shrunk denoise (0) + LoGo(MaxDist): 25890.9463. Comparing optimisations
3.1 Mean-Variance optimisation
First let's see how the denoising and sparsification techniques affect the mean-variance optimisation along the efficient frontier.
using Clarabel
slv = [Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.95)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.9)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.85)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.8)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.75)),
Solver(; name = :clarabel2, solver = Clarabel.Optimizer,
settings = Dict("verbose" => false, "max_step_fraction" => 0.7))]
# JuMP Optimsiers, we will compute the efficient frontier with 50 points for all of them.
opts = [JuMPOptimiser(; pr = prs[1], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[2], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[3], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[4], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[5], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[6], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50)))]
# Mean-Risk estimators using the variance.
mrs = [MeanRisk(; obj = MinimumRisk(), opt = opt) for opt in opts]
# Optimise
ress = optimise.(mrs)6-element Vector{MeanRiskResult{DataType, T2, Vector{OptimisationReturnCode}, Vector{JuMPOptimisationSolution}, JuMP.Model, Nothing} where T2}:
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ LowOrderPrior
│ │ X ┼ 252×20 Matrix{Float64}
│ │ mu ┼ 20-element Vector{Float64}
│ │ sigma ┼ 20×20 Matrix{Float64}
│ │ chol ┼ nothing
│ │ w ┼ nothing
│ │ ens ┼ nothing
│ │ kld ┼ nothing
│ │ ow ┼ nothing
│ │ rr ┼ nothing
│ │ f_mu ┼ nothing
│ │ f_sigma ┼ nothing
│ │ f_w ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ LowOrderPrior
│ │ X ┼ 252×20 Matrix{Float64}
│ │ mu ┼ 20-element Vector{Float64}
│ │ sigma ┼ 20×20 Matrix{Float64}
│ │ chol ┼ nothing
│ │ w ┼ nothing
│ │ ens ┼ nothing
│ │ kld ┼ nothing
│ │ ow ┼ nothing
│ │ rr ┼ nothing
│ │ f_mu ┼ nothing
│ │ f_sigma ┼ nothing
│ │ f_w ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ LowOrderPrior
│ │ X ┼ 252×20 Matrix{Float64}
│ │ mu ┼ 20-element Vector{Float64}
│ │ sigma ┼ 20×20 Matrix{Float64}
│ │ chol ┼ nothing
│ │ w ┼ nothing
│ │ ens ┼ nothing
│ │ kld ┼ nothing
│ │ ow ┼ nothing
│ │ rr ┼ nothing
│ │ f_mu ┼ nothing
│ │ f_sigma ┼ nothing
│ │ f_w ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ FixedDenoise()
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ ShrunkDenoise
│ │ │ │ │ alpha ┴ Float64: 0.0
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ LoGo
│ │ │ │ dist ┼ Distance
│ │ │ │ │ power ┼ nothing
│ │ │ │ │ alg ┴ CanonicalDistance()
│ │ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.QuadExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :G, :bgt, :dev_1, :dev_1_soc, :k, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :variance_flag, :variance_risk_1, :w, :w_lb, :w_ub
fb ┴ nothingLet's plot the efficient frontiers.
using GraphRecipes, StatsPlots
r = Variance()Variance
settings ┼ RiskMeasureSettings
│ scale ┼ Float64: 1.0
│ ub ┼ nothing
│ rke ┴ Bool: true
sigma ┼ nothing
chol ┼ nothing
rc ┼ nothing
alg ┴ SquaredSOCRiskExpr()Vanilla sigma and mu.
plot_stacked_area_composition(ress[1].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Vanilla sigma and mu",
legend = :outerright))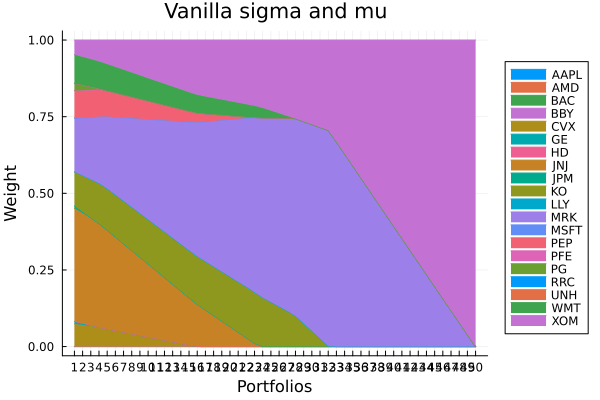
Vanilla sigma and mu.
plot_measures(ress[1].w, prs[1]; x = r, y = ReturnRiskMeasure(; rt = ress[1].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[1].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Vanilla sigma and mu", xlabel = "Variance",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)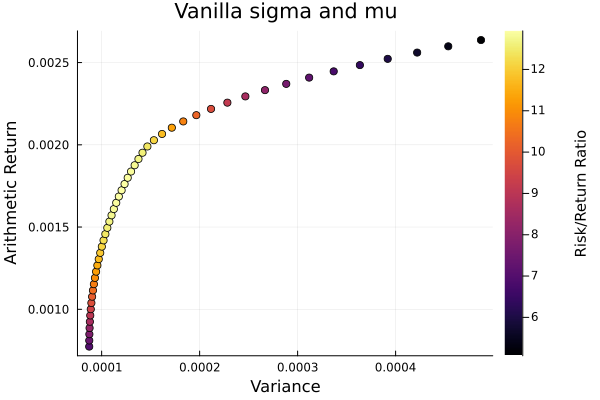
Fixed denoise sigma, BS(VW) mu.
plot_stacked_area_composition(ress[2].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Fixed denoise sigma and BS(VW) mu",
legend = :outerright))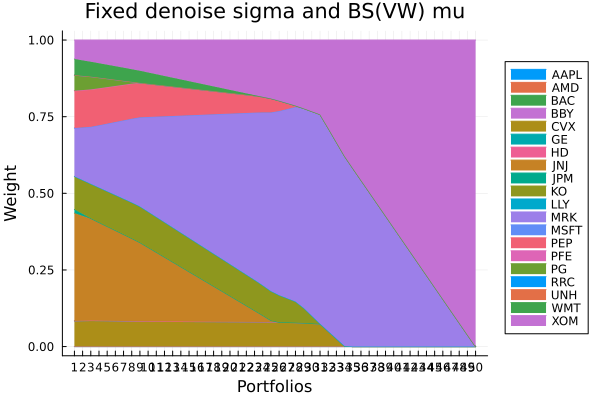
Fixed denoise covariance.
plot_measures(ress[2].w, prs[2]; x = r, y = ReturnRiskMeasure(; rt = ress[2].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[2].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Fixed denoise sigma and BS(VW) mu", xlabel = "Variance",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)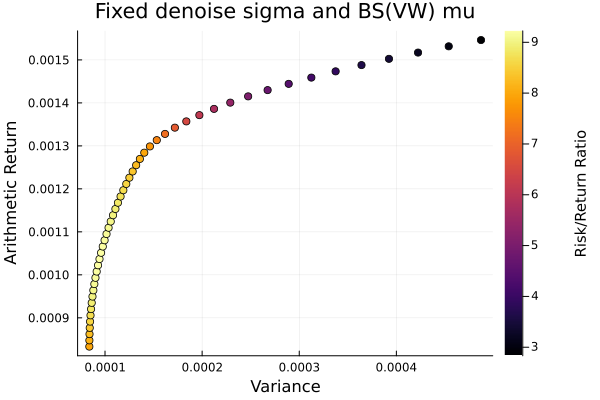
LoGo(MaxDist) sigma and BS(MSE) mu.
plot_stacked_area_composition(ress[3].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "LoGo(MaxDist) sigma and BS(MSE) mu",
legend = :outerright))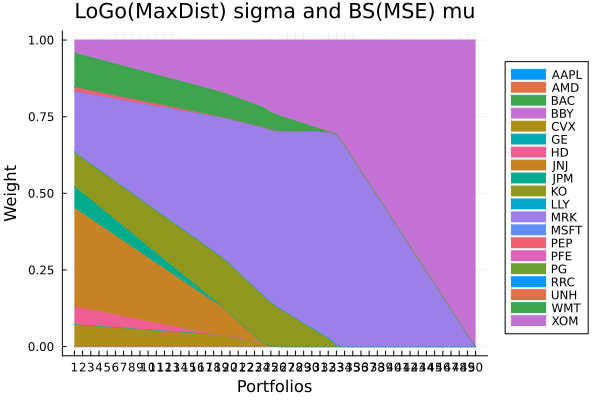
LoGo(MaxDist) covariance.
plot_measures(ress[3].w, prs[3]; x = r, y = ReturnRiskMeasure(; rt = ress[3].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[3].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "LoGo(MaxDist) sigma and BS(MSE) mu", xlabel = "Variance",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)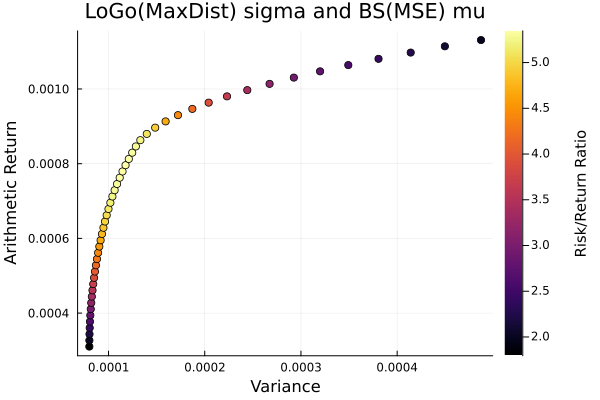
Shrunk denoise (0.5) sigma and BOP(GM) mu.
plot_stacked_area_composition(ress[4].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Shrunk denoise (0.5) sigma and BOP(GM) mu",
legend = :outerright))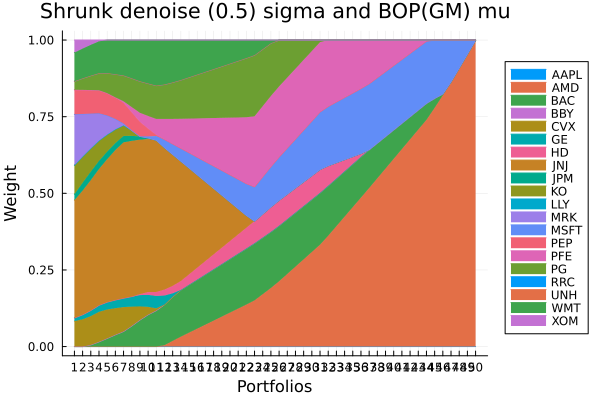
Shrunk denoise (0.5) covariance.
plot_measures(ress[4].w, prs[4]; x = r, y = ReturnRiskMeasure(; rt = ress[4].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[4].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Shrunk denoise (0.5) sigma and BOP(GM) mu", xlabel = "Variance",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)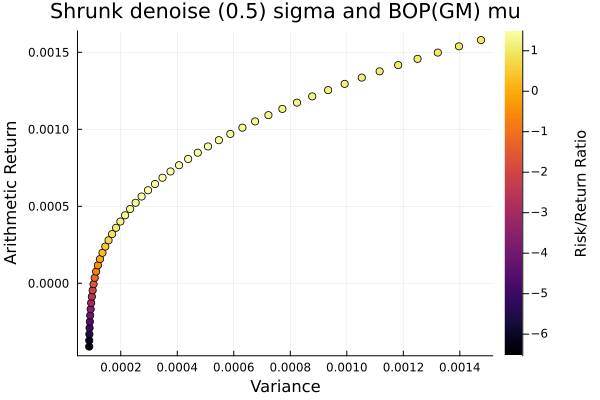
Fixed denoise + LoGo(MaxDist) sigma and BOP(VW) mu.
plot_stacked_area_composition(ress[5].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Fixed denoise + LoGo(MaxDist) sigma and BOP(VW) mu",
legend = :outerright))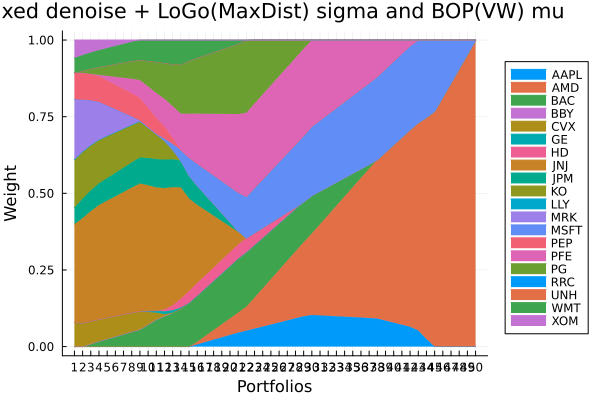
Fixed denoise + LoGo(MaxDist) sigma and BOP(VW) mu.
plot_measures(ress[5].w, prs[5]; x = r, y = ReturnRiskMeasure(; rt = ress[5].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[5].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Fixed denoise + LoGo(MaxDist) sigma and BOP(VW) mu",
xlabel = "Variance", ylabel = "Arithmetic Return",
colorbar_title = "\nRisk/Return Ratio", right_margin = 6Plots.mm)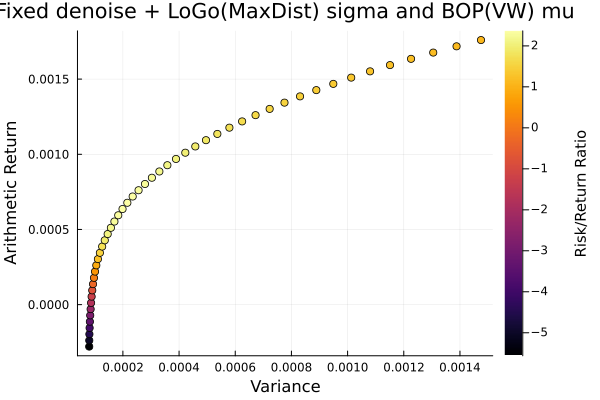
LoGo(ExpDist) sigma and BOP(MSE) mu prior composition.
plot_stacked_area_composition(ress[6].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "LoGo(ExpDist) sigma and BOP(MSE) mu",
legend = :outerright))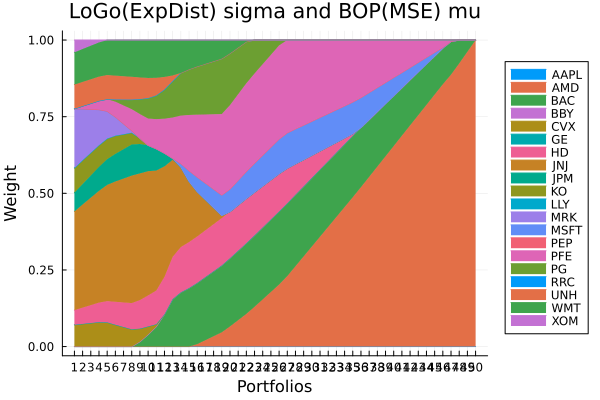
LoGo(ExpDist) sigma and BOP(MSE) mu.
plot_measures(ress[6].w, prs[6]; x = r, y = ReturnRiskMeasure(; rt = ress[6].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[6].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "LoGo(ExpDist) sigma and BOP(MSE) mu", xlabel = "Variance",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)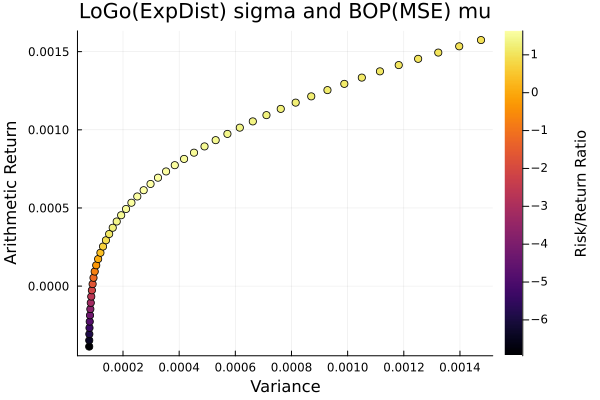
This example is a nice way to show how sensitive moment-based optimisations are to the moment estimation. For now, let's examine how the maximum risk return ratio portfolios differ. An actual analysis would isolate the effect of the covariance and expected returns separately, the point of this example is to show how different ways to improve their estimation and how much the results can be affected by them.
opts = [JuMPOptimiser(; pr = prs[1], slv = slv), JuMPOptimiser(; pr = prs[2], slv = slv),
JuMPOptimiser(; pr = prs[3], slv = slv), JuMPOptimiser(; pr = prs[4], slv = slv),
JuMPOptimiser(; pr = prs[5], slv = slv), JuMPOptimiser(; pr = prs[6], slv = slv)]
# Mean-Risk estimators using the variance.
mrs = [MeanRisk(; obj = MaximumRatio(; rf = 4.2 / 100 / 252), opt = opt) for opt in opts]
# Optimise
ress = optimise.(mrs)
pretty_table(DataFrame("Assets" => rd.nx, "Vanilla" => ress[1].w,
"Fixed + BS(VW)" => ress[2].w,
"LoGo(MaxDist) + BS(MSE)" => ress[3].w,
"Shrunk (0.5) + BOP(GM)" => ress[4].w,
"Fixed + LoGo(MaxDist) + BOP(VW)" => ress[5].w,
"LoGo(ExpDist) + BOP(MSE)" => ress[6].w); formatters = [resfmt])┌────────┬──────────┬────────────────┬─────────────────────────┬────────────────
│ Assets │ Vanilla │ Fixed + BS(VW) │ LoGo(MaxDist) + BS(MSE) │ Shrunk (0.5) ⋯
│ String │ Float64 │ Float64 │ Float64 │ ⋯
├────────┼──────────┼────────────────┼─────────────────────────┼────────────────
│ AAPL │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ AMD │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ BAC │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ BBY │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ CVX │ 0.0 % │ 7.684 % │ 0.0 % │ ⋯
│ GE │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ HD │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ JNJ │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ JPM │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ KO │ 0.0 % │ 5.033 % │ 0.0 % │ ⋯
│ LLY │ 0.002 % │ 0.0 % │ 0.0 % │ ⋯
│ MRK │ 65.977 % │ 65.015 % │ 64.199 % │ ⋯
│ MSFT │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ PEP │ 0.0 % │ 0.001 % │ 0.0 % │ ⋯
│ PFE │ 0.0 % │ 0.0 % │ 0.0 % │ ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴──────────┴────────────────┴─────────────────────────┴────────────────
3 columns and 5 rows omittedPortfolios that emphasise expected returns are more sensitive to the expected returns estimation. It is important to exercise caution when relying on expected returns in particular. If one thinks about it, it summarises all returns information into a single number per asset, so any error in its estimation can have a large effect on the resulting portfolio. We will finish on showing these effects in higher order moment optimisation.
3.2 Mean-NegativeSkewness optimisation
# JuMP Optimsiers, we will compute the efficient frontier with 50 points for all of them.
opts = [JuMPOptimiser(; pr = prs[4], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[5], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[6], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50)))]
r = NegativeSkewness()
# Mean-Risk estimators using the negative skewness.
mrs = [MeanRisk(; r = r, obj = MinimumRisk(), opt = opt) for opt in opts]
# Optimise
ress = optimise.(mrs)3-element Vector{MeanRiskResult{DataType, T2, Vector{OptimisationReturnCode}, Vector{JuMPOptimisationSolution}, JuMP.Model, Nothing} where T2}:
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :GV, :bgt, :cnskew_soc_1, :k, :lw, :nskew_risk_1, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ FixedDenoise()
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :GV, :bgt, :cnskew_soc_1, :k, :lw, :nskew_risk_1, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ ShrunkDenoise
│ │ │ │ │ alpha ┴ Float64: 0.0
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ LoGo
│ │ │ │ dist ┼ Distance
│ │ │ │ │ power ┼ nothing
│ │ │ │ │ alg ┴ CanonicalDistance()
│ │ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 21
│ ├ num_constraints: 5
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ └ Names registered in the model
│ └ :GV, :bgt, :cnskew_soc_1, :k, :lw, :nskew_risk_1, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub
fb ┴ nothingLet's plot the efficient frontiers.
Vanilla V and BOP(GM) mu.
plot_stacked_area_composition(ress[1].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Vanilla V and BOP(GM) mu",
legend = :outerright))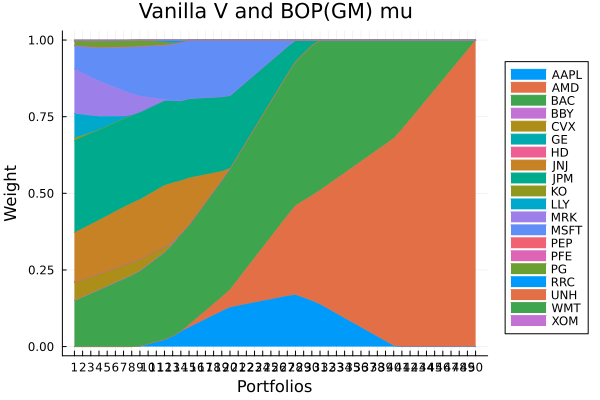
Vanilla V and BOP(GM) mu.
plot_measures(ress[1].w, prs[4]; x = r, y = ReturnRiskMeasure(; rt = ress[1].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[1].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Vanilla V and BOP(GM) mu", xlabel = "Negative Skewness",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)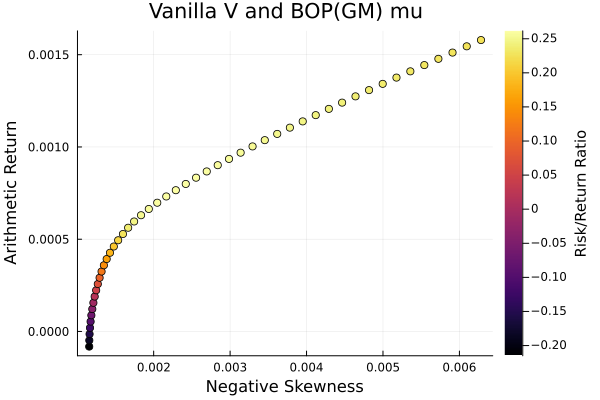
Fixed Denoise V and BOP(VW) mu.
plot_stacked_area_composition(ress[2].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Fixed Denoise V and BOP(VW) mu",
legend = :outerright))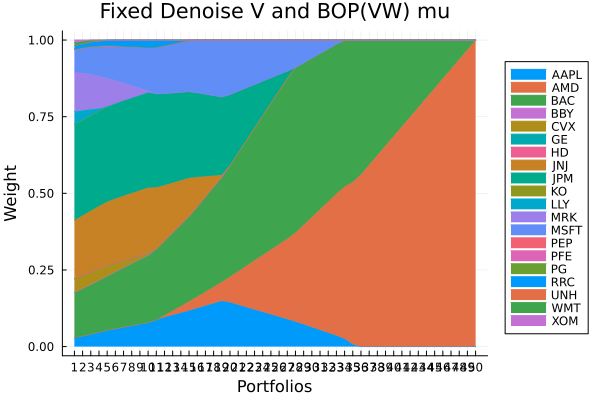
Fixed Denoise V and BOP(VW) mu.
plot_measures(ress[2].w, prs[5]; x = r, y = ReturnRiskMeasure(; rt = ress[2].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[2].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Fixed Denoise V and BOP(VW) mu", xlabel = "Negative Skewness",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)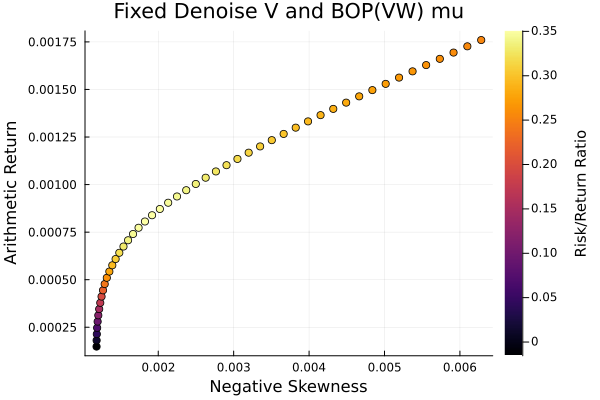
Shrunk(0) Denoise + LoGo(MaxDist) V and BOP(MSE) mu.
plot_stacked_area_composition(ress[3].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Shrunk(0) Denoise + LoGo(MaxDist) V and BOP(MSE) mu",
legend = :outerright))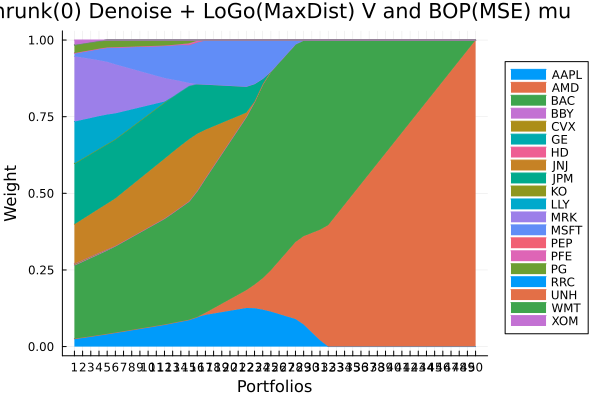
Shrunk(0) Denoise + LoGo(MaxDist) V and BOP(MSE) mu.
plot_measures(ress[3].w, prs[6]; x = r, y = ReturnRiskMeasure(; rt = ress[3].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[3].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Shrunk(0) Denoise + LoGo(MaxDist) V and BOP(MSE) mu",
xlabel = "Negative Skewness", ylabel = "Arithmetic Return",
colorbar_title = "\nRisk/Return Ratio", right_margin = 6Plots.mm)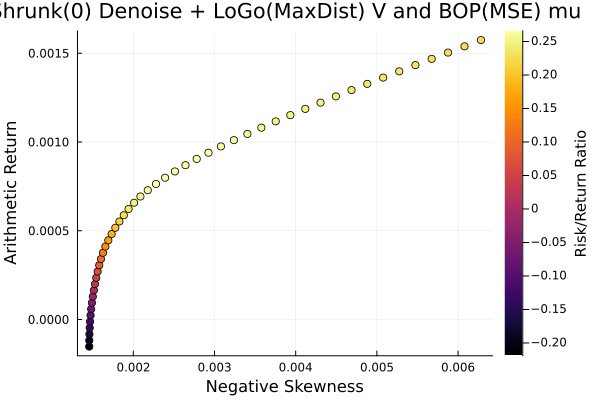
In this case we can se that in this case, these techniques denoising and sparsification make the evolution of the portfolio composition along the efficient frontier smoother.
Now let's examine how the maximum risk return ratio portfolios differ.
opts = [JuMPOptimiser(; pr = prs[4], slv = slv), JuMPOptimiser(; pr = prs[5], slv = slv),
JuMPOptimiser(; pr = prs[6], slv = slv)]
# Mean-Risk estimators using the Negative Skewness.
mrs = [MeanRisk(; r = r, obj = MaximumRatio(; rf = 4.2 / 100 / 252), opt = opt)
for opt in opts]
# Optimise
ress = optimise.(mrs)
pretty_table(DataFrame("Assets" => rd.nx, "Vanilla V + BOP(GM) mu" => ress[1].w,
"Fixed Denoise V + BOP(VW) mu" => ress[2].w,
"Shrunk(0) Denoise + LoGo(MaxDist) V + BOP(MSE) mu" => ress[3].w);
formatters = [resfmt])┌────────┬────────────────────────┬──────────────────────────────┬──────────────
│ Assets │ Vanilla V + BOP(GM) mu │ Fixed Denoise V + BOP(VW) mu │ Shrunk(0) D ⋯
│ String │ Float64 │ Float64 │ ⋯
├────────┼────────────────────────┼──────────────────────────────┼──────────────
│ AAPL │ 16.24 % │ 13.333 % │ ⋯
│ AMD │ 24.414 % │ 11.962 % │ ⋯
│ BAC │ 45.563 % │ 39.701 % │ ⋯
│ BBY │ 0.0 % │ 0.0 % │ ⋯
│ CVX │ 0.0 % │ 0.0 % │ ⋯
│ GE │ 0.0 % │ 0.0 % │ ⋯
│ HD │ 0.0 % │ 0.0 % │ ⋯
│ JNJ │ 0.0 % │ 0.0 % │ ⋯
│ JPM │ 10.307 % │ 18.839 % │ ⋯
│ KO │ 0.0 % │ 0.0 % │ ⋯
│ LLY │ 0.0 % │ 0.0 % │ ⋯
│ MRK │ 0.0 % │ 0.0 % │ ⋯
│ MSFT │ 3.476 % │ 16.165 % │ ⋯
│ PEP │ 0.0 % │ 0.0 % │ ⋯
│ PFE │ 0.0 % │ 0.0 % │ ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴────────────────────────┴──────────────────────────────┴──────────────
1 column and 5 rows omittedSimilarly to the mean-variance case, the more one emphasises the expected returns, the less stable the resulting portfolio. Generally, it's better to use a volatility weighted shrinkage target for the expected returns as that adjusts the expected returns by penalising high volatility and rewarding low volatility assets.
3.3 Mean-Kurtosis optimisation
Finally, we will see how the cokurtosis estimation improvements affect the mean-kurtosis optimisation along the efficient frontier.
# JuMP Optimsiers, we will compute the efficient frontier with 50 points for all of them.
opts = [JuMPOptimiser(; pr = prs[4], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[5], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50))),
JuMPOptimiser(; pr = prs[6], slv = slv,
ret = ArithmeticReturn(; lb = Frontier(; N = 50)))]
r = Kurtosis()
# Mean-Risk estimators using the kurtosis.
mrs = [MeanRisk(; r = r, obj = MinimumRisk(), opt = opt) for opt in opts]
# Optimise
ress = optimise.(mrs)3-element Vector{MeanRiskResult{DataType, T2, Vector{OptimisationReturnCode}, Vector{JuMPOptimisationSolution}, JuMP.Model, Nothing} where T2}:
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ nothing
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 231
│ ├ num_constraints: 6
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.PositiveSemidefiniteConeSquare: 1
│ └ Names registered in the model
│ └ :Gkt, :L2W, :M, :M_PSD, :W, :bgt, :ckurt_soc_1, :k, :kurtosis_risk_1, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub, :x_kurt_1
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ FixedDenoise()
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ nothing
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 231
│ ├ num_constraints: 6
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.PositiveSemidefiniteConeSquare: 1
│ └ Names registered in the model
│ └ :Gkt, :L2W, :M, :M_PSD, :W, :bgt, :ckurt_soc_1, :k, :kurtosis_risk_1, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub, :x_kurt_1
fb ┴ nothing
MeanRiskResult
oe ┼ DataType: DataType
pa ┼ ProcessedJuMPOptimiserAttributes
│ pr ┼ HighOrderPrior
│ │ pr ┼ LowOrderPrior
│ │ │ X ┼ 252×20 Matrix{Float64}
│ │ │ mu ┼ 20-element Vector{Float64}
│ │ │ sigma ┼ 20×20 Matrix{Float64}
│ │ │ chol ┼ nothing
│ │ │ w ┼ nothing
│ │ │ ens ┼ nothing
│ │ │ kld ┼ nothing
│ │ │ ow ┼ nothing
│ │ │ rr ┼ nothing
│ │ │ f_mu ┼ nothing
│ │ │ f_sigma ┼ nothing
│ │ │ f_w ┴ nothing
│ │ kt ┼ 400×400 Matrix{Float64}
│ │ L2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ S2 ┼ 210×400 SparseArrays.SparseMatrixCSC{Int64, Int64}
│ │ sk ┼ 20×400 Matrix{Float64}
│ │ V ┼ 20×20 Matrix{Float64}
│ │ skmp ┼ DenoiseDetoneAlgMatrixProcessing
│ │ │ pdm ┼ Posdef
│ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dn ┼ Denoise
│ │ │ │ alg ┼ ShrunkDenoise
│ │ │ │ │ alpha ┴ Float64: 0.0
│ │ │ │ args ┼ Tuple{}: ()
│ │ │ │ kwargs ┼ @NamedTuple{}: NamedTuple()
│ │ │ │ kernel ┼ typeof(AverageShiftedHistograms.Kernels.gaussian): AverageShiftedHistograms.Kernels.gaussian
│ │ │ │ m ┼ Int64: 10
│ │ │ │ n ┼ Int64: 1000
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ dt ┼ nothing
│ │ │ alg ┼ LoGo
│ │ │ │ dist ┼ Distance
│ │ │ │ │ power ┼ nothing
│ │ │ │ │ alg ┴ CanonicalDistance()
│ │ │ │ sim ┼ MaximumDistanceSimilarity()
│ │ │ │ pdm ┼ Posdef
│ │ │ │ │ alg ┼ UnionAll: NearestCorrelationMatrix.Newton
│ │ │ │ │ kwargs ┴ @NamedTuple{}: NamedTuple()
│ │ │ order ┴ DenoiseDetoneAlg()
│ │ f_kt ┼ nothing
│ │ f_sk ┼ nothing
│ │ f_V ┴ nothing
│ wb ┼ WeightBounds
│ │ lb ┼ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ │ ub ┴ 20-element StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}, Int64}
│ lt ┼ nothing
│ st ┼ nothing
│ lcs ┼ nothing
│ ct ┼ nothing
│ gcard ┼ nothing
│ sgcard ┼ nothing
│ smtx ┼ nothing
│ sgmtx ┼ nothing
│ slt ┼ nothing
│ sst ┼ nothing
│ sglt ┼ nothing
│ sgst ┼ nothing
│ tn ┼ nothing
│ fees ┼ nothing
│ pl ┼ nothing
│ ret ┼ ArithmeticReturn
│ │ ucs ┼ nothing
│ │ lb ┼ Frontier
│ │ │ N ┼ Int64: 50
│ │ │ factor ┼ Int64: 1
│ │ │ flag ┴ Bool: true
│ │ mu ┴ nothing
retcode ┼ 50-element Vector{OptimisationReturnCode}
sol ┼ 50-element Vector{JuMPOptimisationSolution}
model ┼ A JuMP Model
│ ├ solver: Clarabel
│ ├ objective_sense: MIN_SENSE
│ │ └ objective_function_type: JuMP.AffExpr
│ ├ num_variables: 231
│ ├ num_constraints: 6
│ │ ├ JuMP.AffExpr in MOI.EqualTo{Float64}: 1
│ │ ├ JuMP.AffExpr in MOI.GreaterThan{Float64}: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonnegatives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.Nonpositives: 1
│ │ ├ Vector{JuMP.AffExpr} in MOI.SecondOrderCone: 1
│ │ └ Vector{JuMP.AffExpr} in MOI.PositiveSemidefiniteConeSquare: 1
│ └ Names registered in the model
│ └ :Gkt, :L2W, :M, :M_PSD, :W, :bgt, :ckurt_soc_1, :k, :kurtosis_risk_1, :lw, :obj_expr, :ret, :ret_frontier, :ret_lb, :risk, :risk_vec, :sc, :so, :w, :w_lb, :w_ub, :x_kurt_1
fb ┴ nothingLet's plot the efficient frontiers.
Vanilla kt and BOP(GM) mu.
plot_stacked_area_composition(ress[1].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Vanilla kt and BOP(GM) mu",
legend = :outerright))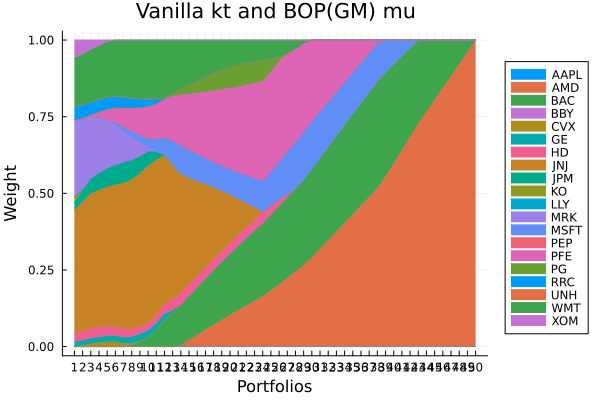
Vanilla kt and BOP(GM) mu.
plot_measures(ress[1].w, prs[4]; x = r, y = ReturnRiskMeasure(; rt = ress[1].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[1].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Vanilla kt and BOP(GM) mu", xlabel = "Kurtosis",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)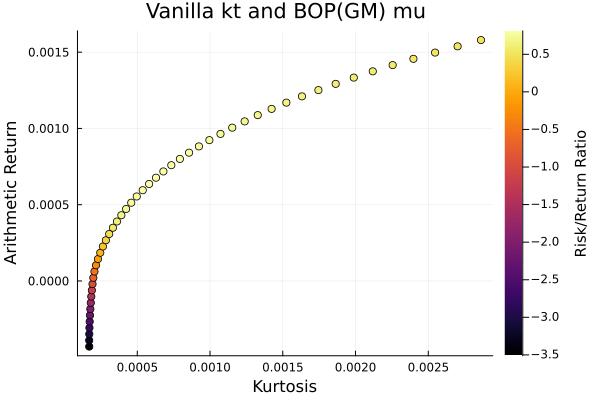
Fixed Denoise kt and BOP(VW) mu.
plot_stacked_area_composition(ress[2].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Fixed Denoise kt and BOP(VW) mu",
legend = :outerright))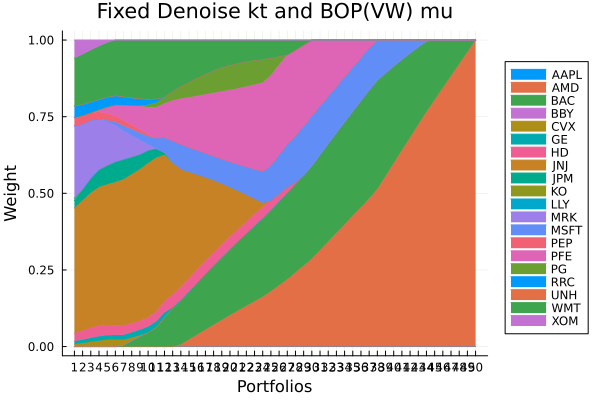
Fixed Denoise kt and BOP(VW) mu.
plot_measures(ress[2].w, prs[5]; x = r, y = ReturnRiskMeasure(; rt = ress[2].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[2].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Fixed Denoise kt and BOP(VW) mu", xlabel = "Kurtosis",
ylabel = "Arithmetic Return", colorbar_title = "\nRisk/Return Ratio",
right_margin = 6Plots.mm)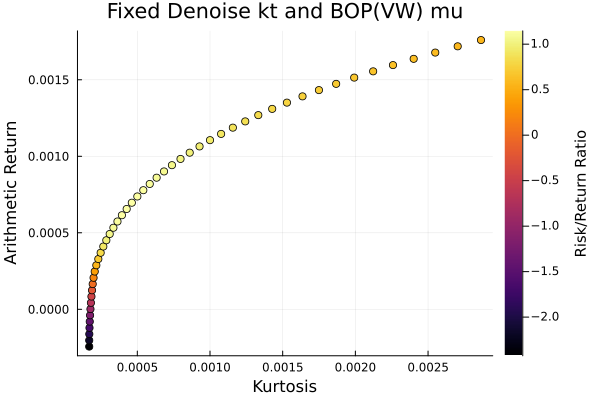
Shrunk(0) Denoise + LoGo(MaxDist) kt and BOP(MSE) mu.
plot_stacked_area_composition(ress[3].w, rd.nx;
kwargs = (; xlabel = "Portfolios", ylabel = "Weight",
title = "Shrunk(0) Denoise + LoGo(MaxDist) kt and BOP(MSE) mu",
legend = :outerright))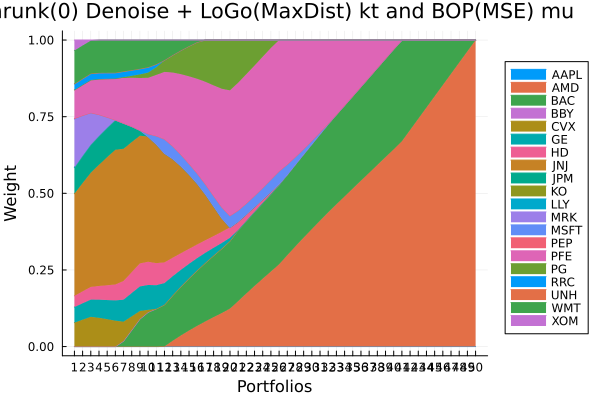
Shrunk(0) Denoise + LoGo(MaxDist) kt and BOP(MSE) mu.
plot_measures(ress[3].w, prs[6]; x = r, y = ReturnRiskMeasure(; rt = ress[3].ret),
c = ReturnRiskRatioRiskMeasure(; rt = ress[3].ret, rk = r,
rf = 4.2 / 100 / 252),
title = "Shrunk(0) Denoise + LoGo(MaxDist) kt and BOP(MSE) mu",
xlabel = "Kurtosis", ylabel = "Arithmetic Return",
colorbar_title = "\nRisk/Return Ratio", right_margin = 6Plots.mm)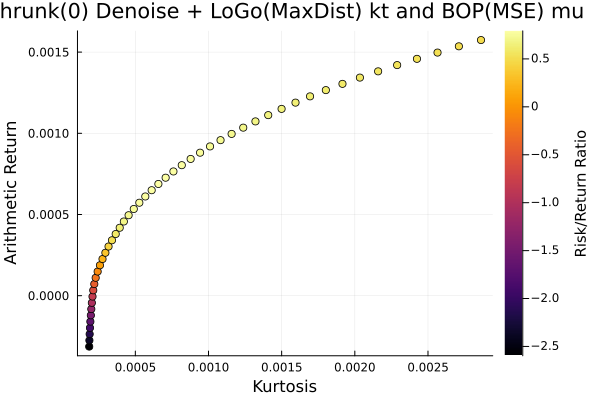
Again, the efficient frontier is smoother, but the kurtosis is inherently less stable than the variance and negative skewness, so the improvements are less pronounced.
Finally let's see what the maximum risk return ratio portfolios look like.
opts = [JuMPOptimiser(; pr = prs[4], slv = slv), JuMPOptimiser(; pr = prs[5], slv = slv),
JuMPOptimiser(; pr = prs[6], slv = slv)]
# Mean-Risk estimators using the Kurtosis.
mrs = [MeanRisk(; r = r, obj = MaximumRatio(; rf = 4.2 / 100 / 252), opt = opt)
for opt in opts]
# Optimise
ress = optimise.(mrs)
pretty_table(DataFrame("Assets" => rd.nx, "Vanilla kt + BOP(GM) mu" => ress[1].w,
"Fixed Denoise kt + BOP(VW) mu" => ress[2].w,
"Shrunk(0) Denoise + LoGo(MaxDist) kt + BOP(MSE) mu" => ress[3].w);
formatters = [resfmt])┌────────┬─────────────────────────┬───────────────────────────────┬────────────
│ Assets │ Vanilla kt + BOP(GM) mu │ Fixed Denoise kt + BOP(VW) mu │ Shrunk(0) ⋯
│ String │ Float64 │ Float64 │ ⋯
├────────┼─────────────────────────┼───────────────────────────────┼────────────
│ AAPL │ 0.0 % │ 0.0 % │ ⋯
│ AMD │ 25.392 % │ 15.762 % │ ⋯
│ BAC │ 27.372 % │ 25.221 % │ ⋯
│ BBY │ 0.0 % │ 0.0 % │ ⋯
│ CVX │ 0.0 % │ 0.0 % │ ⋯
│ GE │ 0.0 % │ 0.0 % │ ⋯
│ HD │ 0.0 % │ 3.799 % │ ⋯
│ JNJ │ 0.0 % │ 2.681 % │ ⋯
│ JPM │ 0.0 % │ 0.0 % │ ⋯
│ KO │ 0.0 % │ 0.0 % │ ⋯
│ LLY │ 0.0 % │ 0.0 % │ ⋯
│ MRK │ 0.0 % │ 0.0 % │ ⋯
│ MSFT │ 15.39 % │ 9.997 % │ ⋯
│ PEP │ 0.0 % │ 0.0 % │ ⋯
│ PFE │ 29.751 % │ 28.446 % │ ⋯
│ ⋮ │ ⋮ │ ⋮ │ ⋱
└────────┴─────────────────────────┴───────────────────────────────┴────────────
1 column and 5 rows omittedGenerally, the volatility weighted target for expected returns combined with fixed denoise, performs quite well. That's not to say other methods are not useful. It's worth using different techniques and comparing the results. For example with cross validation, which is as of yet unimplemented in PortfolioOptimisers.jl. Even so, it's never an exact science. It's always best to combine techniques, which is why we provide users with the ability to use multiple risk measures like in 06_Multiple_Risk_Measures, or to impose constraints on the maximum risk without adding them to the objective function. There are also other ways of directly mitigating these instabilities, such as making use of:
Estimators like [
Stacking]-(@ref), [NearOptimalCentering]-(@ref), and [NestedClusters]-(@ref).Uncertainty sets for the expected returns and covariance matrices.
Logarithmic returns directly in the optimisation.
Regularisation constraints.
Buy-in threshold constraints.
Phylogeny constraints.
Even though those and other techniques do not fix the inherent sensitivity of moment-based optimisations to estimation errors, they can mitigate them.
This page was generated using Literate.jl.